Drone mostra baleias caçando em espiral de Fibonacci, veja

Um drone flagrou o momento que um grupo de (Megaptera novaeangliae) formaram na água a famosa espiral da proporção áurea. O vídeo foi gravado na Antártica, enquanto elas caçavam peixes para se alimentar.

• Os mitos e verdades sobre a proporção áurea
• Baleia-jubarte de 32 toneladas aparece encalhada em Nova York

A concha do caramujo, o rabo do camaleão e várias outras formações da natureza são exemplos que seguem o padrão espiral bastante conhecido. A proporção áurea não é considerada apenas esteticamente agradável, mas também tem fundamentos na matemática.

Assista, no vídeo abaixo:

Fundamentos da matemática

A espiral se baseia no conceito da proporção áurea, derivada da sequência matemática Fibonacci — que recebe o nome de quem a apresentou pela primeira vez, no século 12: Leonardo Fibonacci.

Iniciada com 0 e 1, segue infinitamente, com os números subsequentes sendo sempre o resultado da soma dos dois anteriores. Por exemplo, os primeiros termos são: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 e assim por diante. 

Esses números estabelecem uma proporção cujo valor é aproximadamente 1,618. Ela, por sua vez, é um número irracional infinito, simbolizado na matemática pela letra grega phi: φ. 

Dessa forma, quanto mais a sequência segue, mais a divisão de um número por seu anterior se aproxima dessa proporção, considerada a razão áurea. Então, a sequência matemática foi replicada em um padrão em espiral, como visto na imagem abaixo:

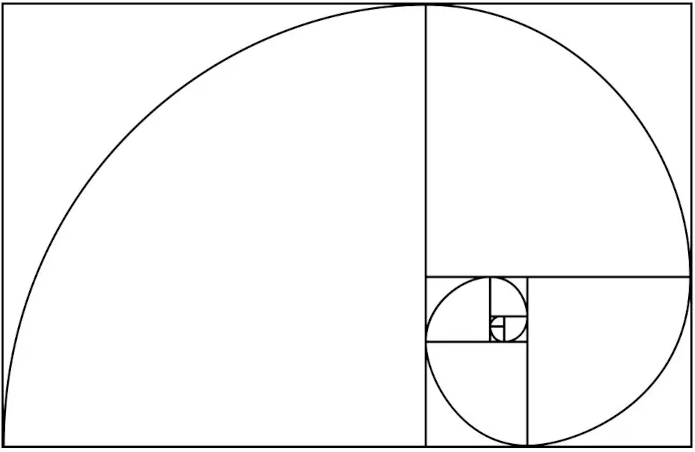
Neste padrão, a imagem se divide em quadrados perfeitamente posicionados. Assim, ao dividir um bloco por outro, o resultado encontrado é a razão áurea, ou seja, o número φ. Isso acontece em qualquer par de quadrados da espiral.

De acordo com pesquisadores das áreas criativas, como arte, arquitetura e design, obras que remontam a espiral de proporção áurea são esteticamente mais agradáveis.

Coincidentemente ou não, essa proporção que segue a sequência de Fibonacci de manifesta em diversos fenômenos naturais. Como, por exemplo, o padrão de caça das baleias jubarte, capturado em vídeo.